Une fois terminé mon article sur la descente de gradient, je me suis rendu compte qu’il manquait deux points important. Le premier concerne l’approche stochastique (SGD) dés lors que l’on a des jeux de données trop importants, le second étant de voir très concrètement ce qui se produit quand on choisit mal la valeur du learning rate. Je vais donc profiter de cet article pour finalement continuer l’article précédent 😉
Stochastique, mais pourquoi ?
Si on se réfère à Wikipédia:
« Le mot stochastique est synonyme d’aléatoire, en référence au hasard et s’oppose par définition au déterminisme. »
Wikipédia
Ok, mais pourquoi parle-t-on ici de processus/choix aléatoire ?
Rappelez-vous dans l’article sur la descente de Gradient, à un moment donné dans l’algorithme nous devons effectuer une somme de toutes les valeurs du jeu de données afin d’évaluer le gradient:
Dans l’exemple que j’avais pris, pas de soucis car on avait vraiment très peu de données. Mais imaginez maintenant que vous ayez des milliers voire des millions de données ! il est clair qu’effectuer ce calcul à chaque itération (epochs) va devenir vitre très coûteux en temps et ressource machine.
Alors au lieu de prendre toutes les données, pourquoi ne pas travailler sur des échantillons à chaque epochs ? On n’aura qu’à choisir ces échantillons de manière aléatoire …
Voilà c’est exactement ce que propose une descente de gradient stochastique(ou SGD). C’est une descente de gradient mais qui va se focaliser sur des échantillons différents du jeu de données global à chaque itération.
Quelles conséquences ?
Rien n’est gratuit ou idéal, et une telle approche a aussi des conséquences que nous allons voir ensemble. Puisque le gradient est calculé sur la base d’échantillons aléatoires il faut garder en tête 2 choses afin de conserver une certaine justesse dans notre algorithme:
- La taille des échantillons (ou mini batchs) est importante et doit être ajustée correctement. On appelle ce paramètre le batch_size. Trop petit il n’est pas représentatif du jeu de données dans l’itération (epochs) et trop grand, et bien il ne présente plus trop d’intérêt !
- Le nombre d’epochs va devoir être naturellement augmenté. En effet étant donné que l’on choisi aléatoirement les batch data (échantillons), il faut être sur de couvrir toutes les données afin une fois de plus d’être représentatif.
Pour résumer, avec la SGD nous avons un hyper-paramètre supplémentaire d’ajustement dans notre algorithme le batch_size.
Voyons ce que ça donne en Python
Le code est globalement le même que celui que nous avons mis en place dans l’article sur la descente de gradient. Nous allons juste y rajouter la notion de batch size et bien sur la sélection aléatoire de données (mini batch).
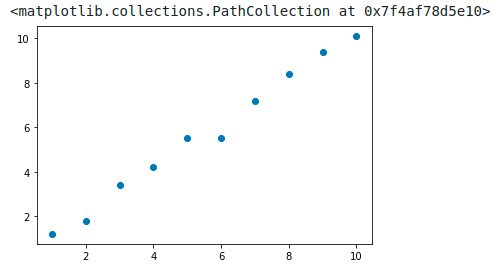
Nous allons juste aussi rajouter quelques données :
X = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0] y = [1.2, 1.8, 3.4, 4.2, 5.5, 5.5, 7.2, 8.4, 9.4, 10.1] plt.scatter(X,y)
Pour la sélection aléatoire de données dans un tableau nous utiliserons la fonction np.random.randint (ci-dessous). Cette méthode sélectionne au hasard des nombres (dans l’exemple ci-dessous) 3 nombres. Ces nombres tirés au hasard sont utilisés ensuite comme des index à partir desquels nous allons récupérer les données su jeu de données global avec la méthode Numpy take().
# Select randomly 3 items index (random from 0 to length)) in the dataset idx = np.random.randint(0, len(X), 3) # take the items by selecting their index np.take(X, idx)
array([4., 1., 1.])Voilà on vient de choisir au hasard 3 points dans le jeu de données. Généralisons ce mécanisme avec notre descente de gradient:
def SGD(_X, _y, _learningrate=0.06, _epochs=5, _batch_size=1):
a, b = 0.2, 0.5
trace = pd.DataFrame(columns=['a', 'b', 'mse'])
for i in range(_epochs):
# stochastic stuff / create batch (data packages) here
indexes = np.random.randint(0, len(_X), _batch_size) # random sample
X = np.take(np.array(_X), indexes)
y = np.take(np.array(_y), indexes)
N = len(X)
delta = y - (a*X + b)
# Updating a and b
a = a - _learningrate * (-2 * X.dot(delta).sum() / N)
b = b - _learningrate * (-2 * delta.sum() / N)
trace = trace.append(pd.DataFrame(data=[[a, b, mean_squared_error(np.array(y), a*np.array(X)+b)]],
columns=['a', 'b', 'mse'],
index=['epoch ' + str(i+1)]))
return a, b, trace
La notion de batch size est implémentée dans les lignes 7, 8 et 9. Remarquez aussi l’ajout du parametre _batch_size qui permet de parametrer la taille des mini-batchs.
Premiers essais
Essayons notre fonction avec les mêmes hyper-paramètres que nous avions utilisés précédemment (cf. article) avec un batch size de 5 (soit la moitié du jeu de données) :
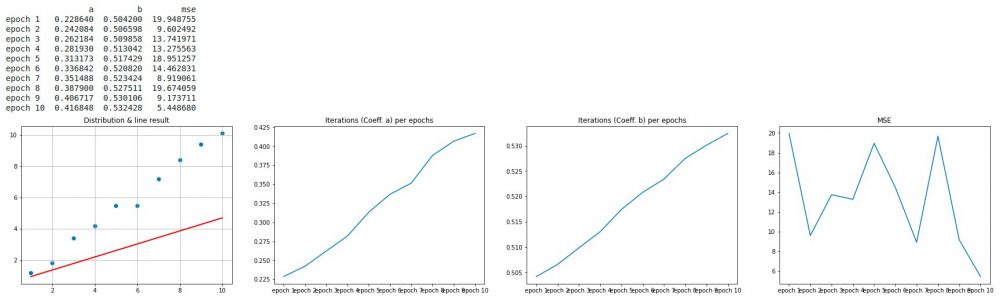
a, b, trace = SGD(X, y, _epochs=10, _batch_size=5, _learningrate=0.06) displayResult(a, b, trace, X, y)
Ouch !
On voit bien que dans le premier graphe la droite (dirigée par les coefficients a et b) est totalement fausse (constatez d’ailleurs les valeurs de a et b après 10 epochs). Mais surtout ce qui doit mettre la puce à l’oreille c’est la courbe de coût (4ème graphe). Le coût explose litérallement à partir de la 7ème itération.
Clairement notre descente de gradient se résume en descente aux enfer !
Choix du Learning rate
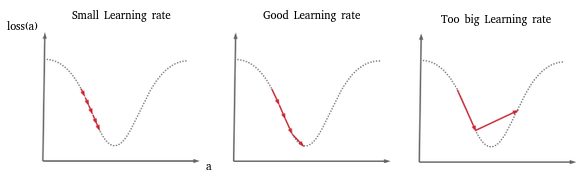
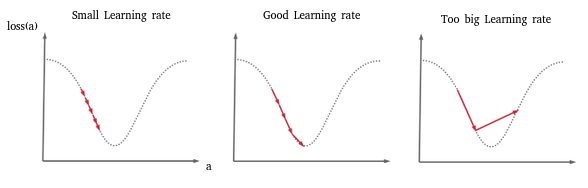
Cet exemple illustre en fait un cas extrême qui peut se produire quand le Learning rate est trop élevé. Lors de la descente de gradient, entre deux pas on saute alors le minimum et même parfois on peut totalement diverger du résultat pour arriver à quelque chose de totalement faux. Le schéma ci-dessous (particulièrement la 3ème image) illustre ce phénomène:
Nous avons donc choisi un learning rate trop fort.
2ème tentative !
Nous allons diminuer fortement ce learning rate pour voir ce que cela donne et pour vérifier notre théorie (on va passer de 0.06 à 0.0005)
a, b, trace = SGD(X, y, _epochs=10, _batch_size=5, _learningrate=0.0005) displayResult(a, b, trace, X, y)
C’est beaucoup mieux mais on voit bien sur le premier graphe que la droite est encore loin d’être la bonne (on devine en effet assez facilement la bonne droite qui devrait être plus inclinée). Par ailleurs la courbe de coût (la 4ème) oscille encore trop, ce qui signifie que notre descente de gradient fait du yoyo entre les deux extrémités de la parabole. Néanmoins on voit bien que la tendance est bonne.
Dernier ajustement
La tendance est bonne, il suffit peut être maintenant de juste laisser le système continuer à s’approcher du minimum. On va donc juste augmenter le nombre d’itération et passer à 100 epochs.
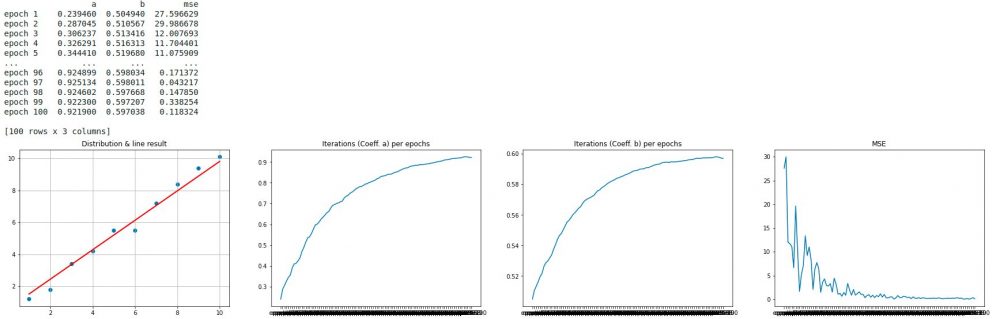
a, b, trace = SGD(X, y, _epochs=100, _batch_size=5, _learningrate=0.0005) displayResult(a, b, trace, X, y)
Génial ! la droite suit globalement bien les points (1er graphe), et on voit bien que le coût a atteint un minimum et surtout reste stable (la courbe s’ecrase pour ne plus jamais remonter). Je crois que l’on peut dire que nous avons bien trouvé nos paramètres a et b !
Conclusion
Dans cet article nous avons vu comment optimiser la descente de gradient dés lors que l’on avait des grands jeux de données (par l’utilisation de mini-batchs) avec la SGD. Certes cela rajoute un nouvel hyper paramètre (batch size), mais quand on aura affaire a des modèles avec plusieurs paramètres et des millions de données, cette option ne sera plus une option justement.
Nous avons ensuite vu les conséquences désastreuse d’un mauvais choix de l’hyper-paramètre learning rate. En jouant sur cet hyper paramètres mais aussi avec le nombre d’itération (epochs) nous avons vu comment nous pouvions ajuster notre descente de gradient.
Ces ajustements sont fondamentaux dès lors que l’on créé un modèle. L’idée de ces article était bien entendu de vous montrer de manière très simpliste comment ils fonctionnent et surtout comment « jouer » avec. Les sources sont aussi disponibles sur Github. N’hésitez pas à faire vos propres expériences.
Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.


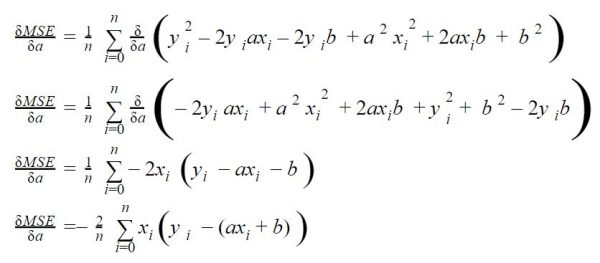

Excellent Article, Excellent Blog , Excellent Site ✅✅✅