Le Machine Learning fait sans doute peur aujourd’hui à cause de son coté boite noire.
Il est vrai que cette approche s’éloigne complètement de l’approche dite traditionnelle à base de règles, qui s’apparente souvent d’ailleurs avec le temps plutôt à un amoncellement d’exceptions autour de règles bien établies. Bref, L’approche « mathématiques » (statistiques / Probabilités) fait peur car nous comprenons difficilement la raison des choix du modèle qui a été conçu. Dans cet article nous allons voir comment ces approches statistiques permettent de trouver quelles variables permettent de déterminer ce ou ces choix du modèle.
C’est finalement bien là l’essence du Machine Learning: Trouver les éléments/variables qui on conduit à faire un choix ou prendre une décision non ? Alors je vous propose de découvrir cette discipline qui tente de donner plus d’explication aux decisions que prennent les modèles de ML: l’eXplainable AI (ou XAI) …
Introduction
Comme d’habitude, je vais utiliser Google colab & Python pour illustrer mes propos.
Pour cet article on va travailler sur des modèles directement interprétables (Régression linéaires, Régressions Logistiques, Random Forest & XGBoost). On appelle aussi ces modèles des modèles GlassBox, car par nature ils produisent les informations nécessaires à leur interpretation (a contrario des modèles de type Black Box). Pourquoi ? tout simplement parce que ces modèles fournissent naturellement et donc sans qu’on leur demande les informations que l’on cherche. Une autre approche consistera à extraire des informations du modèle. Nous irons à ce titre plus loin – mais dans d’autres articles – avec SHAP (Shapley Additive exPlanations) et LIME par exemple.
Voyons déjà ce que ces 3 modèles nous proposent en standard:
- Regression liléaire (sklearn)
- Random Forest (sklearn)
- XGBoost Regression
Récupération du jeu de données
Je vais par ailleurs prendre comme jeu de données le jeu (si connu) des prix immobiliers de Californie founit de base avec Google colab (dans le répertoire /content/sample_data/)
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
import matplotlib.pyplot as plt
import pandas as pd
from google.colab import data_table
# Display smart tables into colab ;-)
data_table.enable_dataframe_formatter()
train = pd.read_csv('/content/sample_data/california_housing_train.csv')
test = pd.read_csv('/content/sample_data/california_housing_test.csv')
all_data = pd.concat([train, test], axis=0)Vous aurez peut être constaté 2 choses:
- Pour commencer l’utilisation de l’objet data_table. C’est un petit plus (une astuce) de Google colab qui vous permet d’afficher un DataFrame de manière beaucoup plus intelligente et dynamique ! essayez et vous allez l’adopter. Vous pourrez naviguer dans votre table, faire des filtres, etc. et le tout directement dans votre Notebook.
- Nous allons concaténer les jeux de données d’entrainement et de test. Pas d’angoisse nous re-diviserons le tout plus tard, mais celà nous permet de vérifier par exemple la qualité des données globales en une seule passe.
Analyse « technique » préalable de nos données
L’enjeu de cet article n’est pas de montrer la phase de préparation de données (plutot l’inverse en fait), néanmoins voyons ce à quoi nous avons à faire:
Regardons nos colonnes :
all_data.columnsIndex(['longitude', 'latitude', 'housing_median_age', 'total_rooms',
'total_bedrooms', 'population', 'households', 'median_income',
'median_house_value'],
dtype='object')Nous avons 8 variables, et l’enjeu du modèle sera de prédire le prix d’une maison ( « median_house_value » ) en fonction d’autres variables comme le nombre de pièces, les coordonnées géographiques, etc.
Seconde étape obligatoire, vérifier que nos données sont bien renseignées (pas de Null !), pour cela une simple technique consiste à faire la somme pour chaque colonne des valeurs nulles:
all_data.isnull().sum()longitude 0
latitude 0
housing_median_age 0
total_rooms 0
total_bedrooms 0
population 0
households 0
median_income 0
median_house_value 0
dtype: int64Si tous les résultats sont à zéro cela signifie que nous n’aurons pas à gérer les trous dans le jeu de données (bonne nouvelle) !
Vérifions maintenant le type des variables :
all_data.dtypeslongitude float64
latitude float64
housing_median_age float64
total_rooms float64
total_bedrooms float64
population float64
households float64
median_income float64
median_house_value float64
dtype: objectExcellent, nous n’avons que des valeurs numériques.
Nous pouvons donc commencer à créer notre modèle…
Rapide Analyse fonctionnelle des données
Il est toujours intéressant de regarder (quand c’est possible) si une relation existe entre le l’étiquette (« median_house_value ») et chacune des variables.
all_data.plot.scatter("median_income", "median_house_value")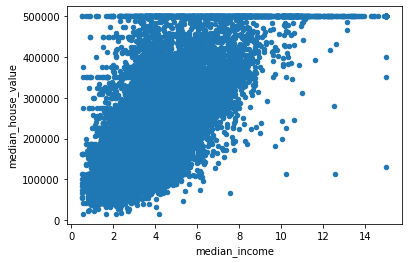
Préparation des données
Avant tout nous devons préparer nos données, pour cela créons une fonction que nous utiliserons pour chaque modèle :
scaler = StandardScaler()
def prepare_data(data, scale=True):
names = data.columns
if (scale == True):
scaled_data = scaler.fit_transform(data)
data = pd.DataFrame(scaled_data, columns=names)
#X_features = ["median_income", "latitude", "longitude", "housing_median_age", "total_bedrooms", "total_rooms", "population", "households"]
y_label = ["median_house_value"]
X = data[names]
del X["median_house_value"]
y = data[y_label]
x_train,x_test,y_train,y_test=train_test_split(X, y, test_size=0.2, random_state=1)
return x_train,x_test,y_train,y_test
x_train, x_test, y_train, y_test = prepare_data(all_data)Notez ici que j’ai mis à l’échelle nos données car elle étaient de nature différente. C’est une étape très importante pour avoir une analyse effective à posteriori de l’influence de chaque varialbes du modèle.
Régression Linéaire
La modélisation d’une regression linéaire avec sklearn est plutôt rapide:
model_1_regression = LinearRegression()
model_1_regression.fit(x_train, y_train)
y_test_prediction = model_1_regression.predict(x_test)
print(f"Score / training data: {round(model_1_regression.score(x_train, y_train)*100, 1)} %")
print(f"Score / test data: {round(model_1_regression.score(x_test, y_test)*100, 1)} %")Score / training data: 64.2 %
Score / test data: 62.3 %Le score est lui plutôt mauvais. Ce n’est pas étonnant quand on voir le graphe précédent et la dispersion des données autour d’une droite potentielle. Un score mérité donc ! mais ce n’est pas vraiment ce qui nous intéresse ici.
Regardons comment chaque variable à influencé le modèle :
def display_feat_imp_reg(reg):
feat_imp_reg = model_1_regression.coef_[0]
reg_feat_importance = pd.DataFrame(columns=["Feature Name", "Feature Importance"])
reg_feat_importance["Feature Name"] = pd.Series(reg.feature_names_in_)
reg_feat_importance["Feature Importance"] = pd.Series(feat_imp_reg)
reg_feat_importance.plot.barh(y="Feature Importance", x="Feature Name", title="Feature importance", color="red")
display_feat_imp_reg(model_1_regression)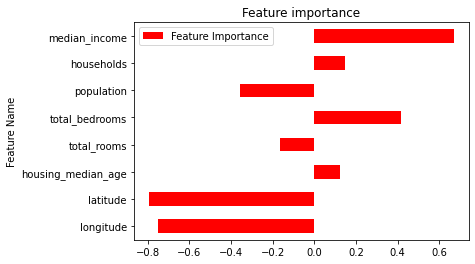
Clairement la variable (colonne) median_income a été la plus influente pour obtenir ce résultat. On voir ensuite que le nombre de chambre est aussi un facteur de choix important juste après.
Ok, voyons maintenant avec un algorithme de type « Random Forest »…
« Random Forest »
Une fois de plus avec sklearn cela ne pose pas de problème et l’entrainement est plutot rapide:
model_2_rforest = RandomForestRegressor()
model_2_rforest.fit(x_train, y_train)
print(f"Score / training data: {round(model_2_rforest.score(x_train, y_train)*100, 1)} %")
print(f"Score / test data: {round(model_2_rforest.score(x_test, y_test)*100, 1)} %")Score / training data: 97.5 %
Score / test data: 81.0 %Sans surprise le score est bien meilleur, mais voyons quelles ont été les variables/colonnes à l’origine de ce score:
def display_feat_imp_rforest(rforest):
feat_imp = rforest.feature_importances_
df_featimp = pd.DataFrame(feat_imp, columns = {"Feature Importance"})
df_featimp["Feature Name"] = x_train.columns
df_featimp = df_featimp.sort_values(by="Feature Importance", ascending=False)
print(df_featimp)
df_featimp.plot.barh(y="Feature Importance", x="Feature Name", title="Feature importance", color="red")
display_feat_imp_rforest(model_2_rforest) Feature Importance Feature Name
7 0.520823 median_income
0 0.160318 longitude
1 0.150686 latitude
2 0.063610 housing_median_age
5 0.034908 population
4 0.026310 total_bedrooms
3 0.024800 total_rooms
6 0.018545 households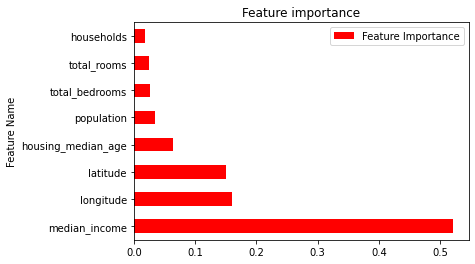
Regression avec XGBoost
Pour finir nous allons utiliser mon petit favori l’algorithme XGBoost pour ce calcul de régression:
model_3_xgboost = XGBRegressor(n_estimators=50,
max_depth=7,
eta=0.1,
subsample=0.7,
colsample_bytree=0.8,
objective ='reg:squarederror')
model_3_xgboost.fit(x_train, y_train)
scores = cross_val_score(model_3_xgboost, x_train, y_train,cv=10)
print("Training Data Mean cross-validation score: %.2f" % scores.mean())
scores = cross_val_score(model_3_xgboost, x_test, y_test,cv=10)
print("Test Data Mean cross-validation score: %.2f" % scores.mean())Training Data Mean cross-validation score: 0.83
Test Data Mean cross-validation score: 0.78Je n’ai pas ajusté les hyperparametres ici (d’où un score très discutable), mais regardons surtout l’influence des variables :
def display_feat_imp_rforest(model):
feature_imp = model_3_xgboost.get_booster().get_score(importance_type='weight')
keys = list(feature_imp.keys())
values = list(feature_imp.values())
data = pd.DataFrame(data=values, index=keys, columns=["score"]).sort_values(by = "score", ascending=False)
data.nlargest(40, columns="score").plot(kind='barh', figsize = (10,5))
display_feat_imp_rforest(model_3_xgboost)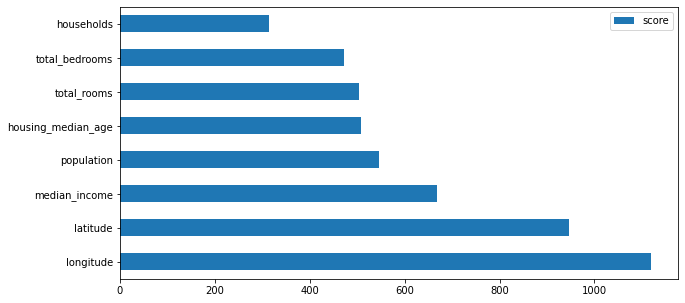
Voilà que l’ordre est encore bouleversé: nous avons maintenant les coordonnées géographiques en première place vient ensuite la variable median_income !
Conclusion
Voilà qui nous donne à réfléchir. Nous avons 3 modèles qui ont donné 3 résultats différents. Et … les scores qui sont aussi différents nous orientent sur l’importance des variable sur un modèle fiable bien sur. A vrai dire ce n’est pas toujours idéal comme approche car pas tellement fiable. On peut être en effet être tenté de le comparer chacun des graphiques que l’on a vu mais il faut garder en tête que chacun des modèles est différent et que donc ils peuvent prendre des décisions de manières totalement différentes (ce que nous avons vu).
Il faut donc avoir une autres approche: calculer la permutation importance par exemple, vérifier la corrélations entre variables, ou encore calculer les valeurs de SHAP (Shapley Additive exPlanations), mais ça c’est une autre histoire que nous verrons dans un autre article.
Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.



Merci pour cet article.
Modèle Régression Linéaire: « Clairement la variable (colonne) median_income a été la plus influente pour obtenir ce résultat. On voir ensuite que le nombre de chambre est aussi un facteur de choix important juste après. » > Il faut interpréter les résultats en prenant la valeur absolue des coefficients. On constate alors que les variables latitude et longitude viennent en première place, et vient ensuite la variable median_income. Ce qui est cohérent avec les résultats obtenus avec XGBoost.