L’objet de cet article est de vous donner les clés afin de bien évaluer votre modèle de classification binaire. Pour cela j’irais vite à l’essentiel car le but n’est pas de déterminer comment choisir tel ou tel algorithme mais bien d’évaluer sa pertinence. Ne vous inquiétez pas car l’aspect choix fera bien sur l’objet d’un prochaine article. Voyons à partir d’un même jeu de données et surtout d’un même travail sur ces données comment nous devons évaluer l’exécution de plusieurs modèles.
Entraînons déjà nos modèles
Pour ce faire nous partirons sur les données kaggle du Titanic (que j’ai déjà utilisé à plusieurs reprises dans mes précédents articles). Téléchargez les ici si vous ne les avez pas encore récupérées. Après quelques préparations, nous y appliquerons 3 algorithmes différents de Machine learning :
- Le classifier « Dummy » (totalement inutile en soi, à part pour servir de base de comparaison)
- la Régression Logistique
- le Random Forest (Forêts aléatoires)
Tout d’abord la préparation des données :
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.dummy import DummyClassifier
titanic = pd.read_csv("../titanic/data/train.csv")
def Prepare_Modele(X, cabin):
target = X.Survived
sexe = pd.get_dummies(X['Sex'], prefix='sex')
cabin = pd.get_dummies(cabin.str[0], prefix='Cabin')
age = X['Age'].fillna(X['Age'].mean())
X = X[['Pclass', 'SibSp']].join(cabin).join(sexe).join(age)
return X, target
cabin = titanic['Cabin'].fillna('X')
X, y = Prepare_Modele(titanic, cabin)Une fois de plus l’objectif n’est pas ici d’expliquer comment les données ont été préparées, je vous renvois pour celà à l’article sur le one-hot notament.
Maintenant entraînons nos modèles, nous obtenons ainsi un scoring global de :
- Le classifier « Dummy » : 53%
- la Régression Logistique : 81 %
- le Random Forest (Forêts aléatoires) : 92%
Précision & Rappel
Un scoring global c’est bien mais dés lors qu’il s’agit de classification il est important d’aller plus loin. En effet si la classification est binaire, les erreurs doivent être évaluées de plus près car l’importance d’un faux positif ne sera pas la même que celle d’un faux négatif. Vous allez sans doute même vouloir faire jouer du curseur entre ces deux types d’erreurs. Mais qu’est-ce qu’un Faux-Positif ? et qui d’un Faux-Négatif ?
Un Faux-Positif est une prédiction positive fausse, un Faux-Négatif c’est une prédiction négative fausse !
Imaginez que vous fassiez un dépistage pour maladie quelconque. Un verdict Faux-Positif vous annonce que vous êtes malade alors que ce n’est pas le cas. Un verdict Faux-Négatif vous annonce que vous n’êtes pas malade … alors que vous l’êtes. Une scoring global pourra être utile mais ce que vous voudrez réellement mesurer c’est le taux de Faux-Négatif car c’est celui-ci qui pourra avoir de grande incidence sur votre prédiction.
Dans le jargon du Machine Learning vous allez vouloir maximiser le rappel !
Comment calculer le rappel, et bien très simplement via cette formule :
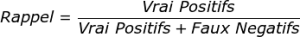
Quant à la précision c’est son pendant :

Un troisième élément mesure l’indicateur f-mesure, vous permet de combiner les deux éléments en un indicateur :
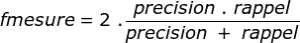
La précision nous permettra notamment de mesurer la capacité du modèle à refuser résultats non-pertinents.
Récupérez tous ces éléments de mesure simplement avec la méthode classification_report (scikit-learn).
Matrice de confusion
Maintenant comment allons-nous récupérer simplement ces Vrais-Faux Positifs-Négatifs ? Et bien tout simplement en utilisant la Matrice de confusion.
Constituer cette matrice est très simple car elle représente justement ces 4 valeurs :
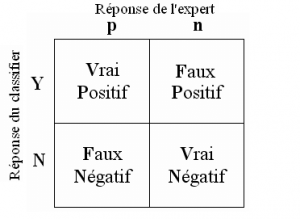
Bien sur scikit-learn vous la fournit très simplement avec la fonction confusion_matrix :
from sklearn.metrics import confusion_matrix
c_dm = confusion_matrix (y, p_dm)
print ("Matrice de confusion / Dummy\n", c_dm)
c_rl = confusion_matrix (y, p_rl)
print ("Matrice de confusion / Reg. Linéaire\n", c_rl)
c_tr = confusion_matrix (y, p_tr)
print ("Matrice de confusion / Random Foret\n", c_tr)Courbe ROC et AUC
Afin d’apporter une touche visuelle et surtout être plus pertinent dans l’analyse un outil efficace est la courbe ROC. Cette courbe vous permet de voir le taux de faux-Positifs par rapport au Vrais Positifs en un clin d’oeil.
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
faux_positifs_rl, vrais_positifs_rl, seuil_rl = roc_curve(y, lr1.decision_function(X))
plt.plot(faux_positifs_rl, vrais_positifs_rl, label="Régression Linéaire")
faux_positifs_tr, vrais_positifs_tr, seuil_tr = roc_curve(y, tree.predict_proba(X)[:,1])
plt.plot(faux_positifs_tr, vrais_positifs_tr, label="Random Forest")
faux_positifs_dm, vrais_positifs_dm, seuil_dm = roc_curve(y, dummy.predict_proba(X)[:,1])
plt.plot(faux_positifs_dm, vrais_positifs_dm, label="Dummy")
plt.xlabel ("Faux positifs")
plt.ylabel ("Vrais positifs")
plt.legend ()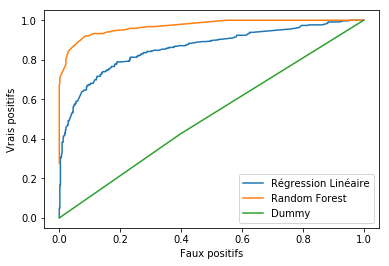
Pour mieux la lire, il faux simplement comprendre que plus la courbe est écrasée vers le bord Haut-Gauche, meilleur le modèle est ! Dans notre exemple c’est plutôt flagrant bien sur, mais parfois nous devrons mesurer la surface sous la courbe pour mesurer précisément.
la surface sous la courbe ROC est la surface AUC.
Pour la mesurer, utilisez la méthode metrics.auc de scikitlearn :
from sklearn import metrics
print ("AUC Dummy: ",metrics.auc(faux_positifs_dm, vrais_positifs_dm))
print ("AUC Reg. linéaire: ",metrics.auc(faux_positifs_rl, vrais_positifs_rl))
print ("AUC Random Forest: ",metrics.auc(faux_positifs_tr, vrais_positifs_tr))Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.



3 Replies to “Evaluer son modèle de classification binaire”