Keras au secours du Titanic ?

Après avoir travaillé les données Kaggle du Titanic dans mes précédents articles (partie 1 et partie 2) je me suis naturellement demandé si on pourrait obtenir de meilleurs résultats en utilisant des techniques de Deep Learning. A première vue et au vue des données (de type structurée) et surtout la taille des jeux de données, je dirais qu’il sera difficile de faire mieux qu’avec les approches traditionnelles.

Bien sur je ne suis pas le premier à tenter l’expérience et vous trouverez d’ailleurs sur le site Kaggle quelques notebooks bien fait et qui s’attaquent à ces données en utilisant ds techniques de Deep learning. En voici un qui est très bien fait par exemple : https://www.kaggle.com/jamesleslie/titanic-neural-network-for-beginners

Keras

Pour cette expérience j’utiliserai donc le framework Keras avec Python qui permet d’aborder ce type de technique en toute simplicité. Pour ceux qui ne connaissent pas ce framework, Keras est une API de Deep learning (réseaux de neurones) de haut niveau. C’est un framework écrit en Python qui est interfaçable avec des APIs de plus bas biveaux comme TensorFlow, CNTK et Theano.

Par défaut Keras utilise Tensorflow (API de Google). Celà veut dire qu’il faut aussi installer cette API sans quoi Keras ne fonctionnera pas !

Installation de Tensorflow

Évidemment je vous recommande de consulter la documentation de Tensorflow ici.

Dans tous les cas l’installation est plutôt simple et s’effectue via pip :

pip install tensorflow

Une fois Tensorflow installé, on peut passer à keras.

Installation de Keras

Installer keras n’est guère plus complexe avec pip :

pip install keras

Préparons nos données avant tout

Nous ferons simple pour ce premier essai, et nous ne récupérons que 6 données/variables :

train = pd.read_csv("../../datasources/titanic/train.csv")
X = train.drop(['Survived', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked' ], axis=1)
X['Pclass'] = X['Pclass'].fillna(5)
X['Age'] = X['Age'].fillna(X['Age'].mean())
X['Fare'] = X['Fare'].fillna(X['Fare'].mean())
y = train['Survived']
X.head()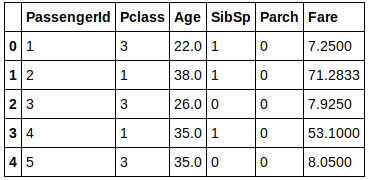

Bien sur nous ne pouvons traiter que des données numériques non nulles.

Notre premier modèle de Deep Learning

La structure de données de base avec Keras est le modèle. Un modèle est en fait une façon d’organiser les couches (concept fondamental dans le deep learning)de votre réseau de neurones. Keras va en fait et tout simplement nous faciliter la vie dans la gestion de ces couches de neurones. Le type de modèle le plus simple que nous allons rencontrer est le modèle séquentiel. C’est bien sur celui que nous utiliserons ici et il est constitué d’un empilement linéaire de couches.

Tout d’abord déclarons les modules Python dont nous aurons besoin (notre fameux modèle et les couches) :

from keras.models import Sequential
from keras.layers import Dense
import pandas as pd

Créons ensuite notre réseau de neurones (modèle séquentiel) composé de 3 couches :

model = Sequential()
model.add(Dense(units=6, activation='relu', input_dim=6))
model.add(Dense(activation="relu", units=100, kernel_initializer="uniform"))
model.add(Dense(activation="sigmoid", units=1, kernel_initializer="uniform"))

Voyez comme ketas s’utilise simplement : On empile tout simplement les couches avec la méthode add(). Le nombre de neurones est déterminé par le parametre units.

La première couche est la couche d’entrée elle permet le mappage avec les variables d’entrées (ici nous aurons 6 variables). La seconde couche est une couche de 100 neurones. la troisième est la couche de sortie qui permet de rendre la « décision », nous utiliserons la fonction « sigmoïd » dans ce cas de figure mais on peut selon le besoin en changer.

Voici à quoi ressemble notre réseau de neurones :

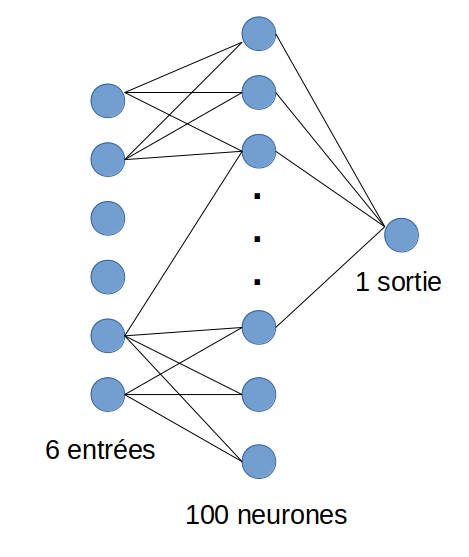
NB: je n’ai pas volontairement dessiné tous les liens inter-neurones, mais sachez qu’ils sont tous reliés les uns aux autres entre chaque couche.

keras nous fournit une fonction qui permet de vérifier le modèle établit :

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_20 (Dense)             (None, 6)                 42        
_________________________________________________________________
dense_21 (Dense)             (None, 100)               700       
_________________________________________________________________
dense_22 (Dense)             (None, 1)                 101       
=================================================================
Total params: 843
Trainable params: 843
Non-trainable params: 0

Entraînons maintenant notre modèle via la fonction fit()

model.fit(X, y, epochs=50, batch_size=30)

A ce moment keras commence a devenir très bavard. Il nous expose en fait le détail ce qui se produit quand il va au travers de Tensorflow calculer tous les poids de tous les neurones (cf. technique de Backpropagation). Mais nous y reviendrons dans un prochain article. Pour l’instant attendons que ce traitement (qui peut être très long) finisse … avec le peu de données que nous avons on ne devrait pas attendre longtemps.

Epoch 1/50
891/891 [==============================] - 0s 470us/step - loss: 0.7276 - acc: 0.5432
Epoch 2/50
891/891 [==============================] - 0s 36us/step - loss: 0.6632 - acc: 0.6184
Epoch 3/50
891/891 [==============================] - 0s 35us/step - loss: 0.6437 - acc: 0.6162
Epoch 4/50
891/891 [==============================] - 0s 33us/step - loss: 0.6302 - acc: 0.6420
Epoch 5/50
891/891 [==============================] - 0s 33us/step - loss: 0.6374 - acc: 0.6498
Epoch 6/50
891/891 [==============================] - 0s 37us/step - loss: 0.6156 - acc: 0.6790
Epoch 7/50
891/891 [==============================] - 0s 32us/step - loss: 0.6128 - acc: 0.6734
Epoch 8/50
891/891 [==============================] - 0s 32us/step - loss: 0.6548 - acc: 0.6431
Epoch 9/50
891/891 [==============================] - 0s 31us/step - loss: 0.6658 - acc: 0.6431
Epoch 10/50
891/891 [==============================] - 0s 32us/step - loss: 0.6375 - acc: 0.6667
Epoch 11/50
891/891 [==============================] - 0s 29us/step - loss: 0.6033 - acc: 0.6857
Epoch 12/50
....

Regardons maintenant notre scoring :

scores = model.evaluate(X, y)
print("\n%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))

891/891 [==============================] - 0s 168us/step

acc: 69.58%

Pas si terrible n’est-ce pas ?

Finalisons

Maintenant nous devons appliquer notre modèle à nos données de test afin de les soumettre à Kaggle :

test = pd.read_csv("../datasources/titanic/test.csv")
Xt = test.drop(['Name', 'Sex', 'Ticket', 'Cabin', 'Embarked' ], axis=1)
Xt['Pclass'] = Xt['Pclass'].fillna(5)
Xt['Age'] = Xt['Age'].fillna(Xt['Age'].mean())
Xt['Fare'] = Xt['Fare'].fillna(Xt['Fare'].mean())

Puis nous allons lancer nos prédiction sur ce modèle :

predictions = model.predict(Xt)

Vous avez remarqué ? les données sont des données décimales allant de 0 à 1, nous allons devoir déterminer un seuil de décision pour avoir un résultat binaire puis ecrire notre résultat dans un fichier:

print([1 if x >= 0.5 else 0 for x in predictions])
final = pd.DataFrame()
final['PassengerId'] = test['PassengerId']
final['Survived'] = [1 if x >= 0.5 else 0 for x in predictions]
final.head()

Il ne vous reste plus qu’à soumettre ce résultat à Kaggle. Mais pour être honnête on a un résultat bien moins interressant qu’avec une approche plus classique de Machine Learning comme on pouvait s’y attendre. Bien sur nous ne traitons que 6 variables, et avec très peu de couches. Voici qui donnera lieu à un prochain article pour voir comment on peut optimiser notre réseau de neurones.

Comme d’habitude vous trouverez tout le code sur Github.

Benoit Cayla

Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.