Traitement d’images (partie 5: Transformations morphologiques)

Dans le précédent chapitre de la série sur le traitement des images nous avons vu quelques transformations basiques d’images comme la rotation ou autres translations. Nous allons voir dans cet article un autre type de transformation (dit « morphologique ») qui peut aussi être considéré comme des filtres. C’est une excellente transition en fait vers le chapitre suivant qui sera dédié, lui aux filtres et plus particulièrement au mécanisme de convolution.

Nous verrons donc dans cet article les principes d’érosion et de dilatation d’images qui sont très utilisés notamment lors de la restauration d’images de mauvaise qualité.

Principe

Les transformations dites morphologiques se basent en fait sur l’application d’un gabarit (ou élément structurant) que l’on va superposer sur chaque pixel de l’image. L’idée est donc très simple, il faut une image (l’image à transformer bien sur), un gabarit (qui est lui aussi une matrice bien sur) qui peut avoir plusieurs formes (étoile, rectangle, etc.) et c’est comme si nous allions utiliser ce gabarit comme un tampon sur l’image que l’on souhaite modifier.

On peut considérer cette opération comme une transformations ou comme un filtre. En effet, la littérature mentionne les deux terminologies, et finalement comme je le disais en introduction cette opération se situe en fait entre les deux concepts.

Voyons comment ces transformations morphologiques fonctionnent avec les deux principales : l’érosion et la dilatation. En réailté il y a 4 grandes opérations morphologiques , à savoir la dilatation, l’érosion, l’ouverture et la fermeture, dans leur version pour les images en niveau de gris (on ne traite pas ici les images couleurs). Néanmoins en ce qui concerne l’ouverture et la fermeture on verra qu’elles dépendent des deux premières dont nous allons détailler le principe ici.

Les gabarits (ou éléments structurants)

Pour effectuer ces transformations on a besoin d’un gabarit qui va en fait nous permettre de servir en quelque sorte d’empreinte sur l’image source. Pour cela nous utiliserons la librairie scikit-image qui va gérer ces transformations morphologiques sans effort. En effet cette librairie propose en standard déjà un certain nombre de gabarits de plusieurs formes (étoile, carré, etc.).

Regardons ici un gabarit tout simple en forme de disque (bon ok sur 3×3 pixels on dirait plutot une croix):

import numpy as np
from skimage import data
import matplotlib as plt
from skimage import morphology
from matplotlib.pyplot import imshow, get_cmap

imshow(morphology.disk(1), cmap=get_cmap('gray'))

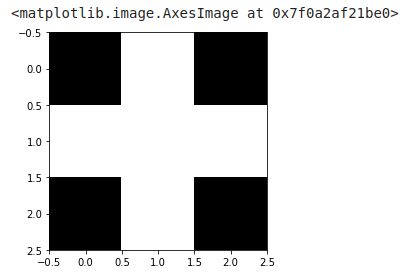
Comme je l’ai expliqué plus haut nous appliquerons ce gabarit sur chaque pixel de l’image cible. En fait nous balayerons chaque pixel et on regardera le résultat de la superposition des pixels de ce gabarit par rapport à l’image.

Dilatation

Commençons par la dilatation (qui correspond à un OU logique sur une image binaire). Pour le coup je trouve que cette transformation porte plutôt bien son nom. En effet, la dilatation permet d’élargir une image. La hauteur et largeur de cette image est donc dilatée seront les sommes des hauteurs et largeurs de l’image originale et du gabarit. Quand nous appliquerons un gabarit sur l’image, on centrera ce gabarit sur chaque pixel et Si le pixel est égal à 1 on fera une empreinte du gabarit sur l’image (centré sur le pixel).

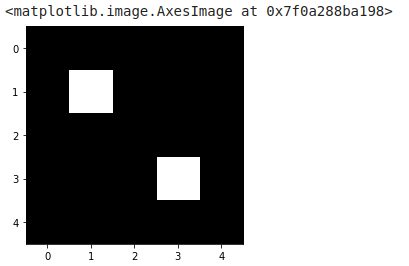
Voyons avec Python comment procéder afin de mieux comprendre le mécanisme avec une image très simple (avec seulement 2 pixels à 1):

image_test = np.array([[0,0,0,0,0], 
                       [0,1,0,0,0], 
                       [0,0,0,0,0], 
                       [0,0,0,1,0], 
                       [0,0,0,0,0]])
imshow(image_test, cmap=get_cmap('gray'))

Appliquons la dilatation avec le gabarit précédent avec la fonction morphology.binary_dilation

dilation = morphology.binary_dilation(image=image_test, 
                                      selem=morphology.disk(1))
imshow(dilation, cmap=get_cmap('gray'))

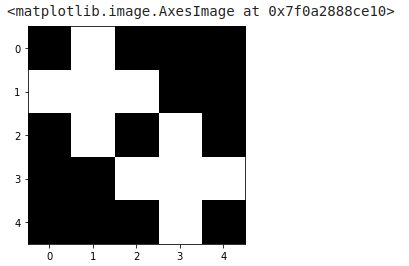
Remarquez dans l’image dilatée l’empreinte des deux pixels originaux avec celle du gabarit. On voit ici deux croix (correspondantes au gabarit) qui sont donc centrées sur les deux pixels originaux que nous avions. On utilise souvent la dilatation pour reconstituer des formes qui sont découpées.

L’érosion

Si vous avez compris le principe de la dilatation, l’érosion n’est guère plus complexe … car c’est tout simplement l’inverse (un ET logique sur une image binaire). Dans le cas de l’érosion on place le gabarit sur chaque pixel. Puis on met le pixel à 1 si tous les pixels du gabarit placé sont 1. Le résultat est donc une réduction de l’image.

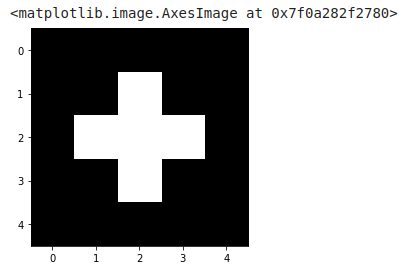
Regardons tout de suite un autre exemple:

image_test = np.array([[0,0,0,0,0], 
                       [0,0,1,0,0], 
                       [0,1,1,1,0], 
                       [0,0,1,0,0], 
                       [0,0,0,0,0]])
imshow(image_test, cmap=get_cmap('gray'))

Appliquons tout de suite une transformation d’érosion avec morphology.binary_erosion

erosion = morphology.binary_erosion(image_test, morphology.disk(1))
imshow(erosion, cmap=get_cmap('gray'))

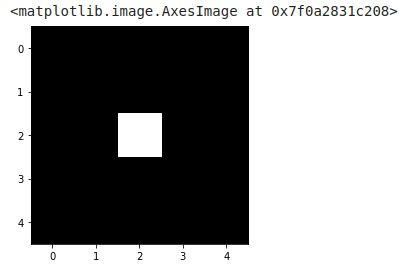
Dans cet exemple simple on voit bien que la seule possibilité pour que tous les pixels du gabarit soient à 1 c’est quand celui là même est centré sur la croix. On utilise souvent l’érosion pour séparer des objets qui sont collés sur une image.

Ouverture & Fermeture

Sans aller dans le détail :

• L’ouverture c’est la composition de l’érosion par un gabarit suivie de la dilatation par ce même gabarit.
• La fermerture c’est la composition de la dilatation par un gabarit suivie de l’érosion par ce même gabarit.

Exemples concrêts

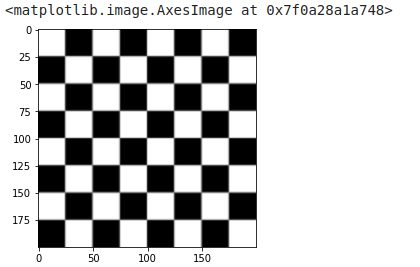
Regardons avec une image ce que cela donne pour l’érosion:

img =  data.checkerboard()
imshow(img, cmap=get_cmap('gray'))

erosion = morphology.binary_erosion(img, morphology.disk(1))
imshow(erosion, cmap=get_cmap('gray'))

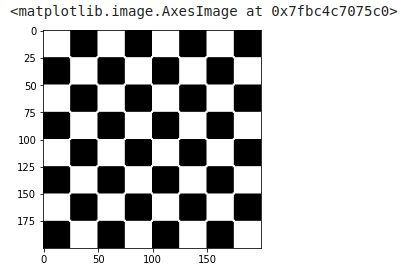
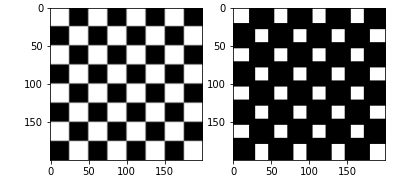
Le résultat n’est pas super visible, il faut regarder de près pour voir la différence. Alors pour mieux voir les effets, on va effectuer plusieurs fois de suite cette transformation et regarder le résultat :

erosion =  data.checkerboard() 
for i in range(5):
  erosion = morphology.binary_erosion(erosion, morphology.disk(1))
imshow(erosion, cmap=get_cmap('gray'))

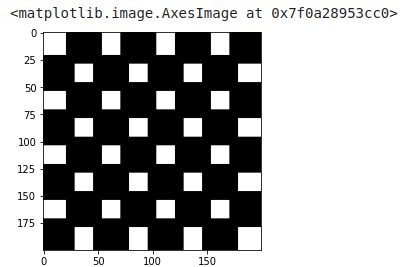
On voit bien mieux avec ce résultat que les pixels noirs prennent de plus en plus plus d’espace.

Voici donc pour les transformations morphologiques, dans le prochain article on abordera les filtres de convolution et leurs applications.