La Régression logistique

Introduction

Pourquoi la régression logistique ? et bien sans doute car cet algorithme est l’un des plus utilisé en Data Sciences. En fait,  certains algorithmes de régression peuvent aussi être utilisés pour de la classification (et inversement bien sur). La régression logistique (ou logit) est souvent utilisée pour estimer la probabilité qu’une observation appartienne à une classe particulière (l’exemple typique est la détection de spam).

Pour résumer c’est un classificateur binaire.

Le principe est simple, si la probabilité estimée est supérieure à 50 %, alors le modèle prédit que l’observation appartient à cette classe (appelée la classe positive, d’étiquette « 1 »), dans le cas contraire, il prédit qu’elle appartient à l’autre classe (la classe négative, d’étiquette « 0 »). tiens ça nous rappelle quelque part comment fonctionne les conversions analogiques – numériques 🙂

Mise en œuvre

Avant tout il nous faut un jeu de données ! je propose de commencer par le grand classique jeu de données du titanic (à télécharger sur le site Kaggle). Ce jeu de données comprend la liste des passagers (survivants ou non : etiquette) avec un certain nombre de caractéristiques (sexe, prix du billet, etc.). C’est parfait pour commencer. Notre objectif ? simple, à partir de ce jeu de données, prédire si un passager avec certaines caractéristiques (les même que le jeu de données bien sur) aurait eu une chance de survivre à ce désastre !

Kaggle.com nous facilite la vie et propose deux jeux de données: un pour entrainer notre modèle et un autre pour le tester (train.csv et test.csv).

Nous utiliserons la boite à outils Python : Scikit-learn (sklearn.linear_model.LogisticRegression)

Observation des données

Avant toute chose nous allons observer les données.

import pandas as pd
titanic = pd.read_csv("./data/train.csv")
titanic.head(5)

Ensuite il est intéressant d’utiliser les fonctions Pandas afin d’introspecter de plus près les données.

Utilisez pour cela les fonctions:

titanic.info()
titanic.describe(include='all')
titanic.PassengerId.describe(include='all')

Voici ce que stockent les colonnes principales ici :

PassengerId	Identifiant du passager (unique)
SisbSp	(Sibling and Spouse) : le nombre de membres de la famille du passager de même génération
Parch	(Parent and Child) : le nombre de membres de la famille du passager de génération différente
Fare	Le prix du ticket
Survived (Etiquette/Label)	Survivant (1) ou pas (0)

Validation croisée avec une régression logistique

Préparons tout d’abord le modèle (ie. la matrice de caractéristiques X ainsi que la matrice d’étiquette y). La fonction Python renvoie ces deux matrices avec seulement 3 caractéristiques (Cf. ci-dessus) :

def Prepare_Modele_1(X):
    target = X.Survived
    X = X[['Fare', 'SibSp', 'Parch']]
    return X, target
X, y = Prepare_Modele_1(titanic.copy())

afin d’affiner notre analyse nous allons lancer des validations croisées sur notre jeux d’entrainement des algorithmes de régression logistique (ici on va lancer 5 validations croisées qui prendrons aléatoirement les 4/5 du jeu global et testerons sur le 1/5 restant):

from sklearn.model_selection import cross_val_score
def myscore(clf, X, y):
    xval = cross_val_score(clf, X, y, cv = 5)
    return xval.mean() *100

Celà permet d’avoir une bonne idée de la fiabilité de notre algorithme. C’est particulièrement pertinent du fait que notre jeu de données est faible !

Pour un premier essai sans effort on obtient un honorable 67.45 %

Essayons une première prédiction …

On peut aussi tester/lancer directement l’algorithme de régression logistique. Tout d’abord on entraine le modèle avec la fonction fit() :

lr2 = LogisticRegression()
lr2.fit(X, y)

Puis on demande des prédictions. pour ce faire il faut bien sur donner à la fonctions predict() la même typologie de vecteurque celui utilisé pour l’entrainer (en gros les mêmes caractéristiques):

lr2.predict([[5.1,1,0]])
lr2.predict([[100.1,1,0]])

Vous remarquerez que le prix du billet semble avoir un impact réel sur la chance de survie.

Par curiosité regardez le scoring de votre modèle :

lr2.score(X, y)

Ici j’ai un score de 68.12%

Nous verrons dans un prochain article comment améliorer notre modèle en ajustant les caractéristiques d’entrainement.

Le notebook Jupyter de cette première partie est disponible sur Github.

Affinons notre modèle en y ajoutant des nouvelles caractéristiques

Caractéristique Classe

Pour celà rien de tel qu’un graphe :

import numpy as np
import matplotlib.pyplot as plt

def plt_feature(feature, bins = 30):
    m = titanic[titanic.Survived == 0][feature].dropna()
    s = titanic[titanic.Survived == 1][feature].dropna()
    plt.hist([m, s], label=['Morts', 'Survivants'], bins = bins)
    plt.legend(loc = 'upper left')
    plt.title('Distribution relative de %s' %feature)
    plt.show()
plt_feature('Pclass')

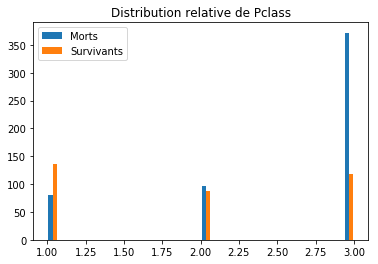
On remarque tout de suite que la notion de classe a bien un lien avec la survie (les personnes de classe 3 ont eu une probabilité de décès bien supérieure que ceux de classe 1 par exemple). C’est donc une caractéristique à prendre en compte. Préparons donc notre nouvelle matrice de caractéristiques et retentons une nouvelle regression logistique

def Prepare_Modele_2(X):
    target = X.Survived
    to_del = ['Name', 'Age', 'Cabin', 'Embarked', 'Survived', 'Ticket', 'Sex']
    for col in to_del : del X[col]
    return X, target
X, y = Prepare_Modele_2(titanic)
myscore(lr1, X, y)

Nous obtenons un score de 67,9 % … Bref décevant, mais plutôt logique finalement, car notre modèle prenait déjà en compte le prix du billet qui a très certainement un lien avec la classe (un billet de 1ere classe est forcément plus cher !).

Caractéristique Sexe

Regardons les histogrammes de répartition par sexe :

parSexe = [1 if passager == 'male' else 0 for passager in titanic.Sex]
titanic["SexCode"] = [1 if passager == 'male' else 0 for passager in titanic.Sex]
m = titanic[titanic.Survived == 0]["SexCode"].dropna()
s = titanic[titanic.Survived == 1]["SexCode"].dropna()
plt.hist([m, s], label=['Morts', 'Survivants'], bins = 30)
plt.legend()

Note: Malheureusement on ne peut pas utiliser de variables catégorielles de type caractères. Pour y remédier on va utiliser les magiques Lists comprehensions de Python pour ajouter une nouvelle colonne à notre liste : [1 if passager == 'male' else 0 for passager in titanic.Sex]

Il semble y avoir un lien entre le sexe et la survie (« les femmes et les enfants d’abord » aurait-il été de mise ce soir là ?). Parfait nous allons ajouter cette variable à notre modèle existant :

def Prepare_Modele_3_Test(X):
    target = X.Survived
    to_del = ['Name', 'Age', 'Cabin', 'Embarked', 'Survived', 'Ticket']
    for col in to_del : del X[col]
    return X, target
X, y = Prepare_Modele_3_Test(titanic.copy())
X.head(5)
myscore(lr1, X, y)

Et là c’est le drame ! une belle erreur Python est retournée stipulant qu’il ne peut pas convertir le Sexe en Float.
ValueError: could not convert string to float: 'male'
C’est bien normal car l’algorithme ne sait que travailler avec des données numériques, il faut donc transformer le sexe en donnée numérique (binaire ici) pour que cela fonctionne :

def Prepare_Modele_3(X):
    target = X.Survived
    sexe = pd.get_dummies(X['Sex'], prefix='sex')
    X = X.join(sexe)
    to_del = ['Name', 'Age', 'Cabin', 'Embarked', 'Survived', 'Ticket', 'Sex']
    for col in to_del : del X[col]
    return X, target
X, y = Prepare_Modele_3(titanic)
myscore(lr1, X, y)

Et là c’est plutôt une bonne surprise car notre score saute de 10 positions pour atteindre 79,4%

Pondération des caractéristiques/variables

Il peut être interressant de voir la pondération des caractéristiques (cad l’importance que l’algorithme leur donne), pour celà il suffit d’afficher l’attribut de LogisticRegression() comme suit :

lr1.fit(X, y)
lr1.coef_

(Attention la pondération n’est calculée qu’après un appel à fit(), si vous ne faites pas cet appel vous aurez une erreur !)

Voici le résultat : array([[ 1.20981540e-04, -7.76272690e-01, -2.48122601e-01, -8.67013029e-02, 4.01693066e-03, 1.85813513e+00, -8.29102327e-01]])

Chaque élément du vecteur ci-dessous indique la pondération de la variable du modèle (une valeur positive augmente la probabilité une négative la diminue).

Note: On pourra ajouter d’autres variables pour affiner encore plus évidemment : jouer sur l’age par exemple et plus généralement sur la qualité des données (valeurs manquantes, etc.).

Conclusion

Nous avons vu dans cet article comment une régression logistique pouvait nous aider à déterminer (classifier) un diagnostique binaire. Cet algorithme est d’ailleurs très utilisé en médecine. Nous avons aussi constaté qu’avant de changer d’algorithme ou de méthode il était indispensable en premier lieu d’affiner les caractéristiques (ajout, modification, etc.): c’est le feature ingeneering. Enfin, ajouter des caractéristiques liées n’avait que peu d’impact sur le résultat (on verra que c’est d’autant plus vrai, voire obligatoire dans le cas d’algorithmes comme Naives Bayes).

Le notebook Jupyter de cette seconde partie est disponible sur Github